大人が意外と解けない数学「？に当てはまる数字を求めなさい」

今回は、長方形と三角形が組み合わさった図形の面積に関する問題です。

三角形が加わることで少し複雑に見えますが、使用する公式は少ないので計算自体は簡単です。

ひらめきが重要なので、柔軟に考えてみてください。

この問題に取り組んだ後には、きっと頭が以前よりも柔軟になっているはずです。

問題

問題
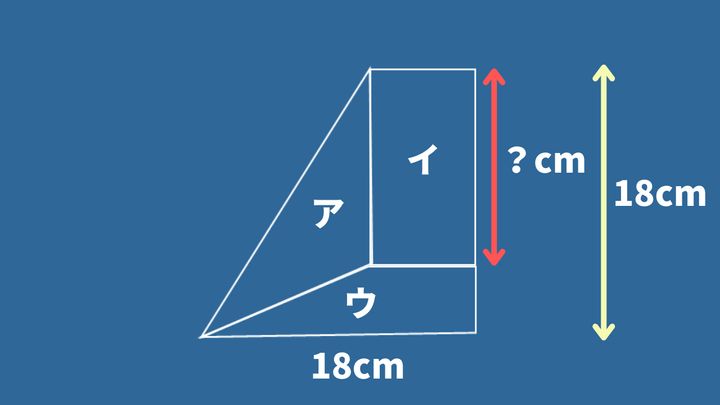
？に当てはまる数字を求めなさい。（図の中の赤線の部分の長さ）
※ア・イ・ウの面積はそれぞれ等しいものとする。

今回の問題では、「補助線」を使います。どこに引くかがポイントです。

解説

答えは「12cm」です。

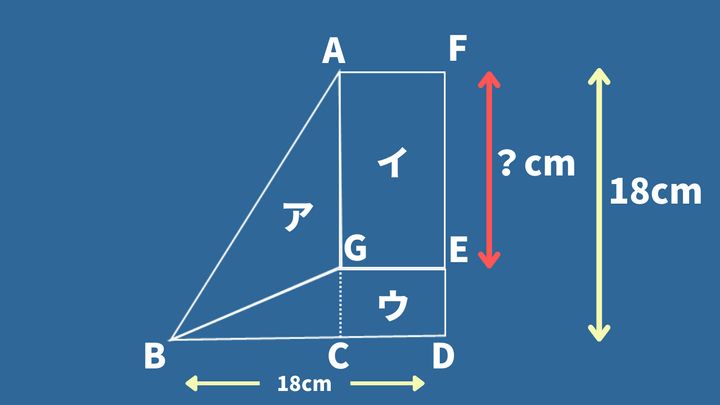
それでは、補助線を加えた図をもとに解説していきます。

まずは、全体の図形を見ていきましょう。

全体の図形は台形で、高さと下底が18cmと分かっているので、上底の長さAFを使って面積を表すことができます。

台形の面積＝（上底+下底）×高さ÷ 2

台形の面積の公式より

(AF+18)×18÷2
＝9(AF+18)

と表すことができました。ア・イ・ウはこれを三等分しているという条件なので、

ア＝イ＝ウ＝3(AF+18)・・・(1)

となります。

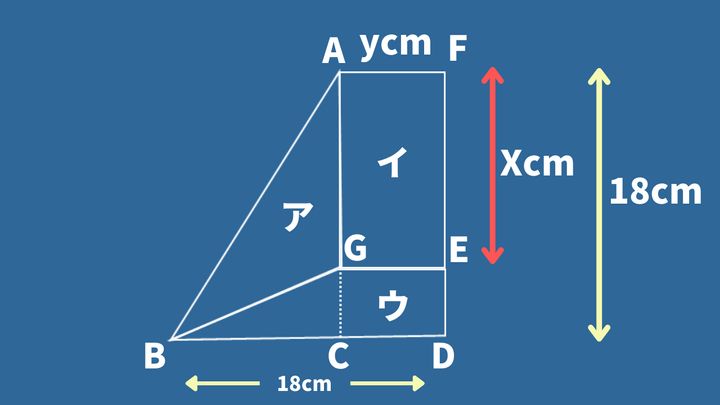
アは三角形なので、AGを底辺、BCを高さとして捉えると「AG×BC÷2」と表すことができますが、AGとBCはそれぞれFEと18-AFと等しくなっています。

つまり、アの面積はFE＝x、AF＝yを用いて

x(18-y)÷2
＝(18x-xy)/2・・・(2)

ということですね。

続いてイの面積ですが、長方形なので「AF × FE＝xy」と表せます・・・(3)

xとyという二つの未知数に対して式が二つできましたので、(2)と(3)を見比べると計算が進みそうですね。

(アの面積)=(イの面積)より
(18x-xy)/2＝xy
両辺を2倍して
18x-xy=2xy
18x=3xy
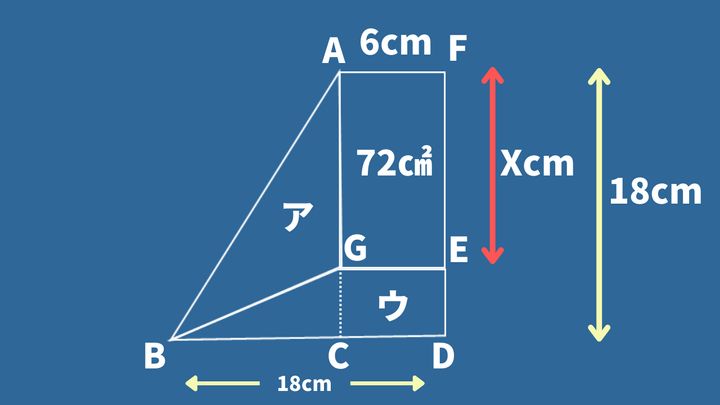
y＝6

y＝AF＝6を求めることができたので、(1)を用いてイの面積は3(6+18)＝72と分かります。

最後に、イの横の長さは6、面積は72なので縦を表すFEは、72÷6＝12となります。

まとめ

複雑な図形も、補助線を引くことで解答への糸口が生まれました。

計算力よりも発想力やひらめき力が重要になってくる問題でしたね。

大人になった今こそ、頭の体操としてぜひ図形問題に挑戦してみてください。

※当メディアでご紹介する数学関連記事において、複数の解法を持つものもございます。 あくまでも一例のご紹介に留まることを、ご了承ください。

---

 文・編集（監修）：うおうお  
数学の教員免許を活かし、個別指導・集団指導の学習塾で主に数学の講師として小学生から高校生までを指導。現在は民間学童保育所で放課後児童支援員として勤務しながらフリーランスで受験指導もしている。日々、小学生の宿題指導を通して算数の魅力を深掘りし楽しく伝えている。

---

面積パズルをもう一問どうぞ！