算数・数学の図形問題のひとつである「角度を求める問題」。
三角形や四角形という形の他にもいろいろな図形が扱われます。
今回はそんな角度に関する問題に挑戦してみましょう。
問題
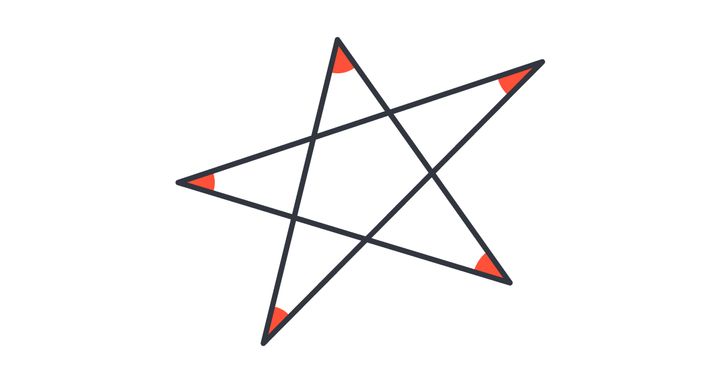
次の図において、印のついた角の大きさの和を求めなさい。
星型の図形の5つの角の大きさの和を求める問題です。
ひとつひとつの角の大きさは分かっていないのに、どうやってたし算するの!?と思われるかもしれませんが、きちんと求めることができるのです。
さて、今回の問題の答えは「180度」です。
解説
ひとつひとつの角の大きさは分かっていません。そのため、単純にたし算はできません。
そこで、ポイントになるのは「角度が等しい別の角に帰着させる」ということです。
詳しく説明しますね。
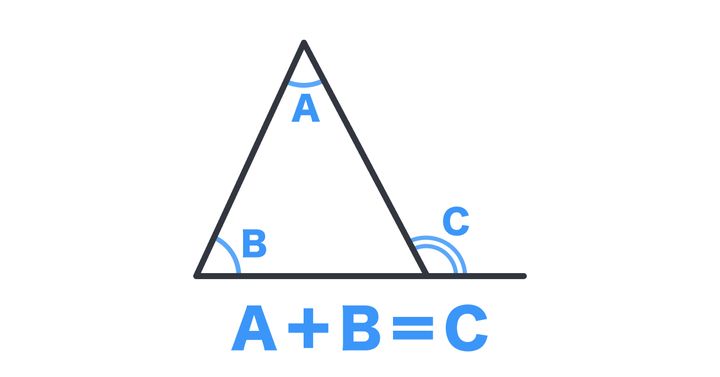
例えば三角形において「三角形の1つの外角は、それと隣り合わない2つの内角の和に等しい」ということが分かっています。
図で見ると下の通りです。これを「外角の定理」と言います。
ひとつひとつの角の大きさは分かっていませんが、2つの角を足して、ひとつの角にまとめてしまうことができます。
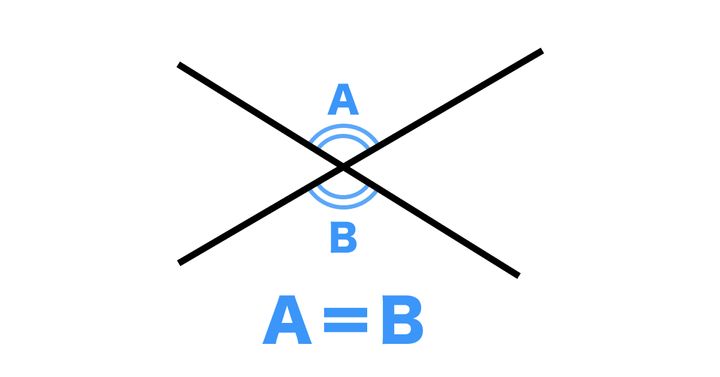
そして、問題を解くためにはもうひとつ「対頂角は等しい」ということも利用します。
2本の交わる線で作られる角のうち、向かい合う角同士は等しいというものです。
それでは、今回の問題を見てみましょう。
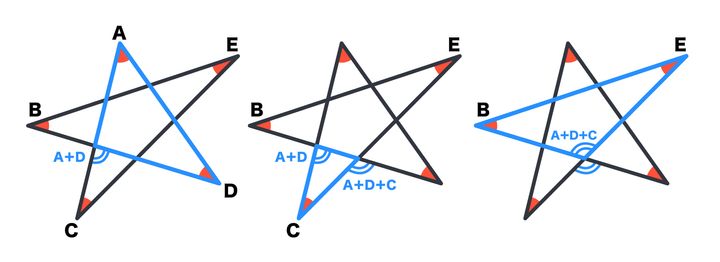
外角の定理をうまく使うと、別のところに「たし算の形で角の大きさ」を表すことができています。
最終的には、「B+E+(A+D+C)」=「A+B+C+D+E」で三角形の内角の和となりました。
したがって、その和は180度ということになります。
まとめ
ひとつひとつの角は分からないけど、全体にすると求めることができるという問題でした。
パズルのように角度の和を求めていくのが面白いですね。
ひらめきも大切ですが、少しの知識があると、より楽しく考えることができます。
文・監修:SAJIMA
日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」。
編集:TRILLニュース