図形の問題は“ひらめき”が大事！直線lと直線mが平行のときの∠xは値は？

図形の問題は「ひらめき」が大切！

一見すると簡単そうな図でも、意外と苦戦することもあります。しかし、そんな苦戦した図形の問題も、たった1本の補助線を引くだけで、すぐに解けてしまいます。

この1本の補助線をどこに引くのかというのが、図形問題のセンスです！

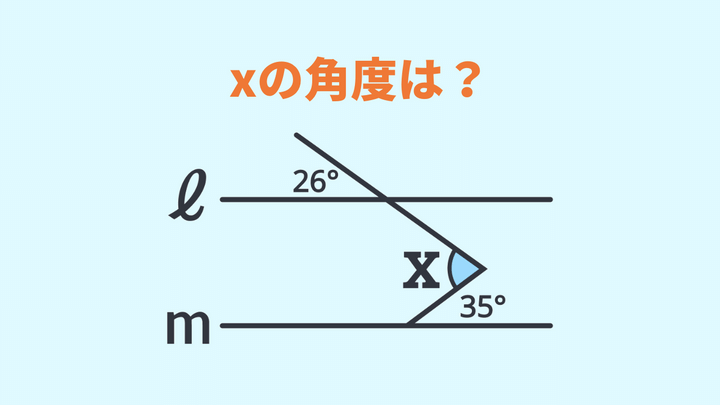
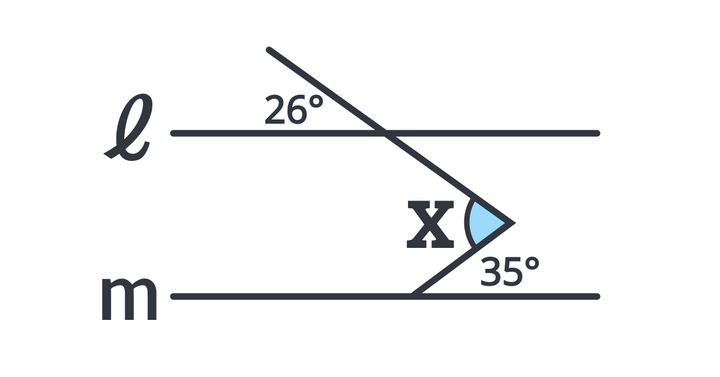
次の図で、直線lと直線mが平行のとき、∠xの大きさを求めよ。

図形の角度を求める問題といえば、「三角形の内角の和は180度」とか「四角形の内角の和は360°」などを使うような問題を覚えている人も多いのではないでしょうか。

問題の図の中に三角形や四角形のような図形はなく、2本の平行線と”くの字型”の線。そこから∠xの大きさを求めないといけません。

ヒントは1本の補助線。どこかに線を加えるだけで、問題が解きやすくなります。

この補助線をどこに書き加えるかがポイントです。

さて、角度を求めることはできたでしょうか。

答えは、「61°」です。

まず、補助線はどこに引けばいいのかを考えましょう。

もしかすると、三角形や四角形が作れるように線を引こうとした方もいるのではないでしょうか。

今回は平行線の問題です。「平行線の性質」を利用して問題を解きます。

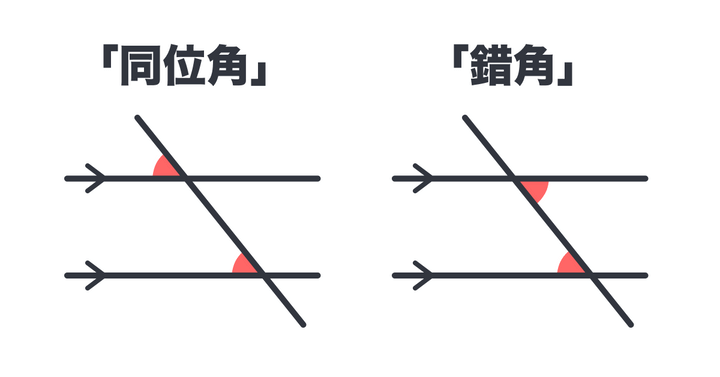
図のように、2直線にほかの1本の直線が交わってできる角のうち、同じ位置にある2つの角を同位角、斜め向かいにある角を錯角といいます。
そして、2直線が平行のとき、同位角と錯角はそれぞれ等しい角度になるという性質があるのです。

今回の問題の図は、途中で”くの字型”に折れ曲がっているので、このままでは同位角も錯角もできていません。

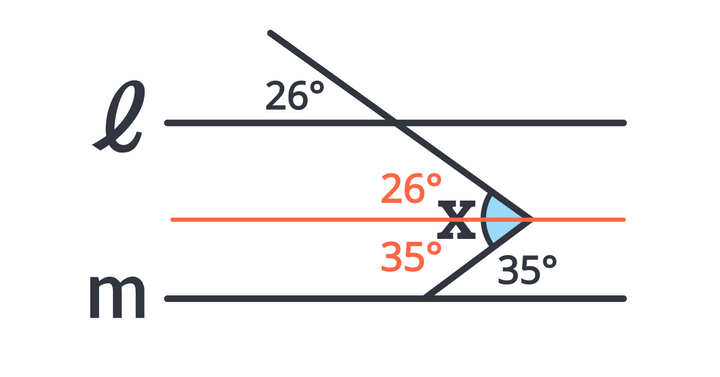
そこで、頂点を通るように、直線l、mと平行な線を引いてみましょう。

すると、求めるべき∠xは2つに分かれてしまいますが、上部は同位角、下部は錯角を用いて求めることができるようになりました。

上部は同位角より26°、下部は錯角より35°。

∠x＝26＋35 ＝61となり、角度は61°です。

同位角や錯角が等しくなるという平行線の性質を利用した図形の問題でした。

最終的に、角度の計算はとても簡単なので、補助線が引くことができるかが、今回の問題のポイントです。

冒頭では「図形の問題はひらめきが大切」と言いましたが、なにも「天から降りてきたひらめき」という訳ではありません。

平行線の性質を知っていれば、自ずと補助線を引くところも決まってくるはずです。

知識とひらめきは表裏一体のような関係ですね。

文・監修：SAJIMA

日本国内外の学校、学習塾で数学・理科の講師として幼児から高校生までを指導。現在はフリーランスとして独立し、オンラインを中心に授業を展開している。子供への学習指導だけでなく、大人向けの数学講座も開講し、算数・数学の楽しさを広く伝える活動を行っている。日本数学検定協会認定「数学インストラクター」。

編集：TRILLニュース編集部